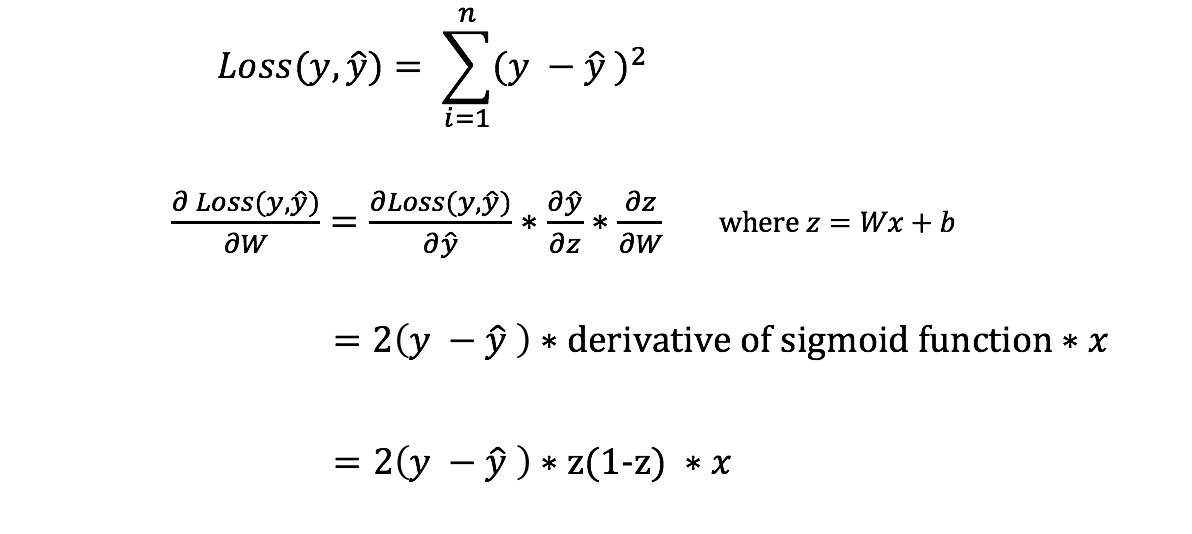O que é uma rede neural?
A maioria dos textos introdutórios para Redes Neurais traz analogias cerebrais ao descrevê-las. Sem me aprofundar nas analogias do cérebro, acho mais fácil simplesmente descrever as Redes Neurais como uma função matemática que mapeia uma dada entrada para uma saída desejada.
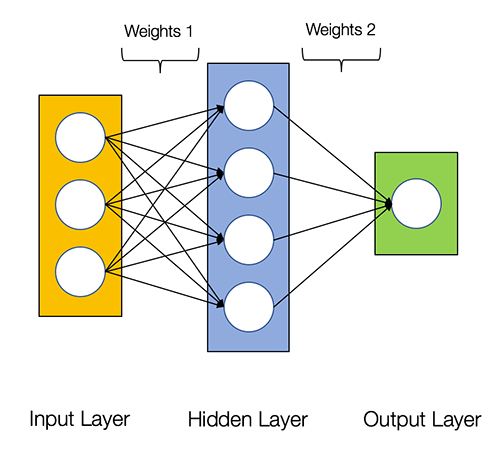
Redes Neurais consistem nos seguintes componentes
- Uma camada de entrada , x
- Uma quantidade arbitrária de camadas ocultas
- Uma camada de saída , ŷ
- Um conjunto de pesos e vieses entre cada camada, W e b
- Uma escolha da função de ativação para cada camada oculta, σ . Neste tutorial, usaremos uma função de ativação Sigmoid.
O diagrama abaixo mostra a arquitetura de uma rede neural de 2 camadas ( observe que a camada de entrada é normalmente excluída quando se conta o número de camadas em uma rede neural )
Criar uma classe de rede neural no Python é fácil.
Treinando a Rede Neural
A saída ŷ de uma rede neural simples de 2 camadas é:
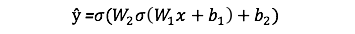
Você pode notar que na equação acima, os pesos W e os biases b são as únicas variáveis que afetam a saída ŷ.
Naturalmente, os valores corretos para os pesos e vieses determinam a força das previsões. O processo de ajuste fino dos pesos e vieses dos dados de entrada é conhecido como treinamento da Rede Neural.
Cada iteração do processo de treinamento consiste nas seguintes etapas:
- Calculando a saída prevista ŷ , conhecida como feedforward
- Atualizando os pesos e vieses, conhecidos como backpropagation
O gráfico sequencial abaixo ilustra o processo.
Feedforward
Como vimos no gráfico sequencial acima, feedforward é apenas um cálculo simples e, para uma rede neural básica de 2 camadas, a saída da Rede Neural é:
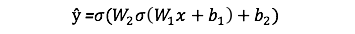
Vamos adicionar uma função feedforward em nosso código python para fazer exatamente isso. Note que, por simplicidade, assumimos que os vieses sejam 0.
No entanto, ainda precisamos de uma maneira de avaliar a “bondade” de nossas previsões (ou seja, quão longe estão as nossas previsões)? A função de perda nos permite fazer exatamente isso.
Função de perda
Existem muitas funções de perda disponíveis, e a natureza do nosso problema deve ditar a nossa escolha da função de perda. Neste tutorial, usaremos um erro simples de soma de quadrados como nossa função de perda.
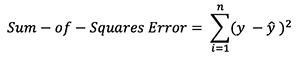
Ou seja, o erro de soma dos quadrados é simplesmente a soma da diferença entre cada valor previsto e o valor real. A diferença é quadrada para medirmos o valor absoluto da diferença.
Nosso objetivo no treinamento é encontrar o melhor conjunto de pesos e vieses que minimiza a função de perda.
Retropropagação
Agora que medimos o erro de nossa previsão (perda), precisamos encontrar uma maneira de propagar o erro de volta e atualizar nossos pesos e vieses.
Para saber a quantidade apropriada para ajustar os pesos e vieses, precisamos conhecer a derivada da função de perda em relação aos pesos e vieses .
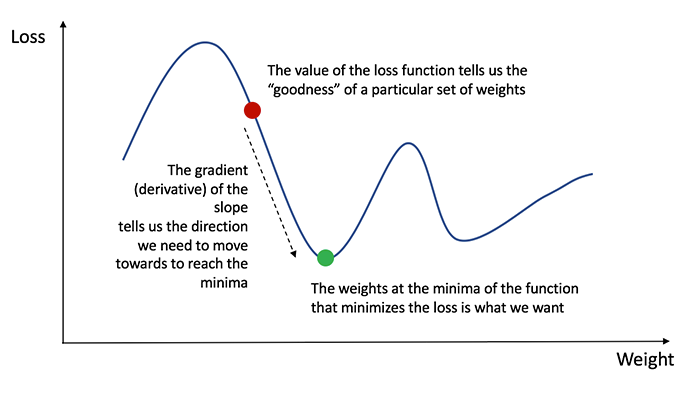
Lembre-se do cálculo de que a derivada de uma função é simplesmente a inclinação da função.
Se tivermos a derivada, podemos simplesmente atualizar os pesos e vieses aumentando / reduzindo com ela (consulte o diagrama acima). Isso é conhecido como descida de gradiente .
No entanto, não podemos calcular diretamente a derivada da função de perda em relação aos pesos e vieses porque a equação da função de perda não contém os pesos e vieses. Portanto, precisamos da regra da cadeia para nos ajudar a calcular isso.
Ufa! Isso foi feio, mas nos permite obter o que precisávamos - a derivada (inclinação) da função de perda em relação aos pesos, para que possamos ajustar os pesos de acordo.
Agora que temos isso, vamos adicionar a função backpropagation ao nosso código python.
Para uma compreensão mais profunda da aplicação do cálculo e da regra da cadeia na retropropagação, eu recomendo fortemente este tutorial por 3Blue1Brown.
Colocando tudo junto
Agora que temos nosso código Python completo para fazer feedforward e backpropagation, vamos aplicar nossa Rede Neural em um exemplo e ver como ela funciona.
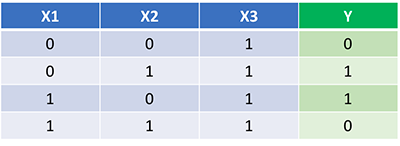
Nossa Rede Neural deve aprender o conjunto ideal de pesos para representar essa função. Note que não é exatamente trivial para nós calcular os pesos apenas por inspeção.
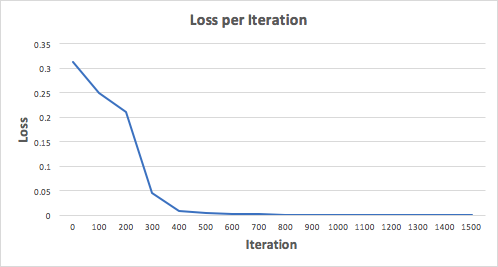
Vamos treinar a rede neural para 1500 iterações e ver o que acontece. Olhando para o gráfico de perda por iteração abaixo, podemos ver claramente a perda monotonicamente decrescente no mínimo. Isso é consistente com o algoritmo de descida de gradiente que discutimos anteriormente.
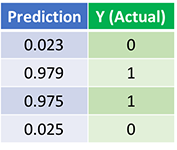
Vamos ver a previsão final (saída) da Rede Neural após 1500 iterações.
Nós fizemos isso! Nosso algoritmo de feedforward e backpropagation treinou a Rede Neural com sucesso e as previsões convergiram nos valores verdadeiros.
Observe que há uma pequena diferença entre as previsões e os valores reais. Isso é desejável, pois impede o overfitting e permite que a Rede Neural generalize melhor os dados não vistos.
Qual é o próximo?
Felizmente para nós, nossa jornada não acabou. Ainda há muito a aprender sobre Redes Neurais e Aprendizado Profundo. Por exemplo:
- Que outra função de ativação podemos usar além da função Sigmoid?
- Usando uma taxa de aprendizagem ao treinar a rede neural
- Usando convoluções para tarefas de classificação de imagem
Eu estarei escrevendo mais sobre esses tópicos em breve, então siga-me no Medium e fique de olho neles!